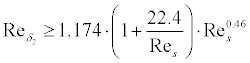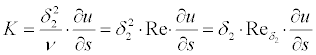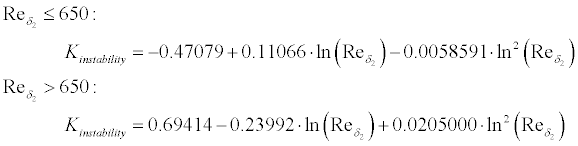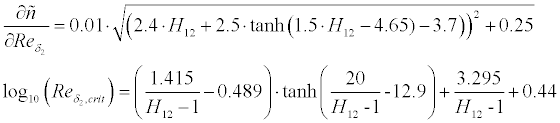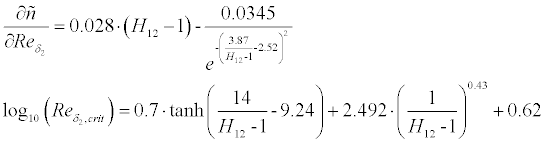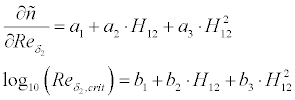The Boundary Layer Method

In order to calculate the friction drag of an airfoil for a given flow condition (angle of attack, Reynolds number), an analysis of the viscous boundary layer is necessary. From the momentum loss in this small layer on the surface of the airfoil the drag can be derived. As the velocity distribution changes with angle of attack, the drag changes too. Also, the thickness of the boundary layer changes with Reynolds number.

The boundary layer module uses the velocity distribution derived by the panel method and performs its calculations based on the formulas presented in [14, 15, 16]. The method is a so called integral boundary layer method, which does not handle laminar separation bubbles or large scale separation (stall). The boundary layer module works best in the Reynolds number regime between 500'000 and 20'000'000.
The results of the boundary layer module are also used to correct lift, drag and moment coefficients empirically, if separation occurs. Additionally, a blending to separated, flat plate coefficients is performed for very high angles of attack.

The procedure starts at the stagnation point and marches along each surface, integrating simplified boundary layer equations. The integration follows a 2nd order Runge-Kutta scheme with stabilization by automatic step reduction. This can be a bit slow some times, but works more reliable than the simple Newton method used before. During the way towards the trailing edge, the method checks, whether transition from laminar to turbulent or separation occurs.

The following empirical transition criteria have been implemented and can be selected by the user:

Method	Transition assumed when	Recommendation
Eppler 1[14]		Re > 1x105
Eppler 2 [17]		Re > 1x105
Michel 1 [35]		Re > 2x106
Michel 2		Re > 2x106
Granville	Here, an additional local pressure gradient parameter K is used ("Pohlhausen parameter") Instability is assumed when K > Kinstability In regions of instability, transition is assumed when K > Ktransition	Re > 5x106
Drela en  approximation (Xfoil pre 1991)	approximation of n transition can occur when
Drela en  approximation (Xfoil post 1991) [36]	approximation of n transition can occur when Note: Depending on the version of Xfoil, The last constant in the second equation has been changed several times between 0.62 and 0.7.
Arnal en  approximation by Würz	approximation of n transition can occur when Note: The coefficients ai and bi can be found in [37] (as well as an interesting discussion of empirical transition models).

If laminar separation is detected, the method switches to turbulent flow and continues. When turbulent separation is found, the boundary layer integration is stopped and an empirical drag penalty depending on the length of the separated region is added to the result.

Flow State	Separation assumed when
laminar
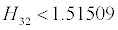turbulent

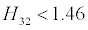The drag is applied by examining the boundary layer parameters at the trailing edge, using the so called Squire-Young formula.

Tabular Output

The tables produced on the Boundary-Layer card contain the following columns:

For abbreviations see the quick reference page.

Last modification of this page: 21.05.18

[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.

Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.

It might take some time until you receive an answer and in some cases you may even receive no answer at all. I apologize for this, but my spare time is limited. If you have not lost patience, you might want to send me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose. Any statements may be incorrect and unsuitable for practical usage. I cannot take any responsibility for actions you perform based on data, assumptions, calculations etc. taken from this web page.

© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this document for a publication, you have to cite the source. A publication of a recompilation of the given material is not allowed, if the resulting product is sold for more than the production costs.

This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.

This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.

Impressum       Datenschutz