Propulsion by Propellers
Propulsion by PropellersAs Newton stated, "actio est reactio". For the propulsion
problem, this means that a device accelerating air or water in one direction,
feels a force in the opposite direction. A propeller accelerates incoming air
particles, "throwing" them towards the rear of the airplane, and thus
feels a force on itself - this force is called thrust. Looking more
closely at propellers shows, that a propeller adds a velocity 
to then incoming velocity v. The first half of this acceleration takes
place in front of the propeller, and the second half behind the propeller.
Because the mass of air passing through the stream tube must be constant
(conservation of mass), the increased velocity leads to a contraction of the
stream tube passing through the propeller disk (neglecting compressibility).
 |
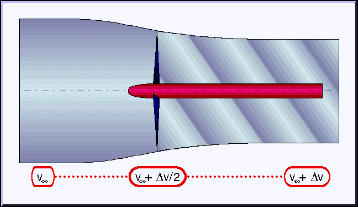Side view of the stream tube passing through a propeller, showing the acceleration in front and behind the propeller. The propeller also induces swirl into it's wake. |
Besides the contraction of the stream tube, a propeller also adds a swirl component to its outflow (wake). The amount of swirl depends on the rotational speed of the engine and eats up energy, which is not available for thrust anymore. Typical, well designed propellers loose about 1% to 5% of their power in the swirl of the propeller wake. The swirl angle (about 1°...10°) may cause non symmetrical flow conditions on parts behind the propeller, e.g. at the tailplanes.
The stream tube of a low bypass ratio turbo jet engine looks completely different, because the acceleration of the flow is mainly performed through the thermal expansion of the heated air. Here the incoming stream tube will usually have a smaller diameter than the exhaust stream, depending on operating conditions. The final extreme is the rocket engine, which has no incoming stream tube, but creates its exhaust jet only by expanding the gases created by a chemical reaction (e.g. by burning a fuel/oxygen mixture). The total mass contained in the exhaust flow is carried inside the rocket (fuel plus oxydator).
The Thrust of a propeller depends on the volume of air (or water) accelerated per time unit, on the amount of the acceleration, and on the density of the medium. Based on momentum considerations, it can be expressed by the following formula:
(1)
|
where: |
|
||||||||||||||||||
Examining the quite simple formula reveals, that the thrust T
increases when the diameter D increases (the first term is the area of
the propeller "disk") or when the density 
of the medium increases. The acceleration of
a propeller depends on the velocity v, thus it is generally not true
that increasing the velocity v increases the thrust. But it can be
said, that increasing the additional velocity ,
increases the thrust. For a propeller of a fixed diameter, working in a certain
medium at a certain speed, thrust depends on the velocity increase
only.
Power is defined as force times distance per time. Using the available thrust T to drive a vehicle at a certain speed v (which already is distance per time) we can calculate the propulsive power (sometimes also called available power) from:
. (2)
Now, thrust ist the one thing, the power to create this thrust the other. Of course we want to create as much thrust as possible from the smallest amount of power, which can be expressed by the term efficiency.
Efficiency of a propeller is defined as the ratio of available power to the engine power which is
. (3)
Note, that this definition for efficiency contains the velocity v, which means, that the efficiency approaches zero as the flight speed goes to zero, because the thrust cannot become infinitely large. So this definition is not useful for the special case of static thrust.
Neglecting rotational losses, the power absorbed by the propeller can also be expressed by
, (4)
which can be used to combine the equations above into a relation between the velocity and the efficiency for a given power and diameter:
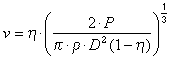. (5)
Unfortunately this equation cannot be easily solved for 
,
but below, we find the relation plotted to find the efficiency
for given values of power P, diameter D and density .
This efficiency could be achieved by an optimum propeller in its design point,
if there were no induced and friction losses - it is the upper limit of what you
can expect from a perfect propeller. In reality the efficiency will be 10 to 15%
less than this value, only highly efficient propellers, operating under light
loading conditions P/D² come close to this theoretical limit.
For a given power P, it is always desirable to use the largest possible propeller diameter D, which may be limited by mechanical restrictions (landing gear height) or aerodynamic constraints (tip Mach number). That's why most man or solar powered airplanes use large, slowly turning props. These catch a large volume of air and accelerate it only slightly to achieve the maximum efficiency.
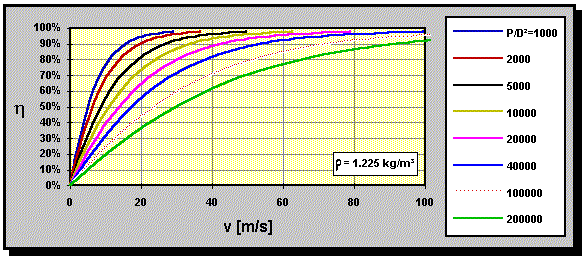
Optimum efficiency according to momentum theory versus flight
speed for different power loadings P/D² in [W/m²].
The density of the air is assumed to be 1.225 kg/m³. Curves have been
calculated by equation (5).
Example:
The speed of an airplane model flying straight and level at full throttle has
been measured to be 252 km/h. The efficiency
of the propeller is assumed to be 80%. From bench tests at the same
rotational speed the engine power is known to be 1.5 kW. The
propeller diameter is 0.25 m and the density of air 1.225 kg/m³.
What is the thrust generated by the engine/propeller combo at the given flight
speed? How big is the additional velocity induced by the propeller to generate
the thrust? Is the assumed efficiency reasonable?
The speed of the model is 252/3.6 = 70 m/s. Using the assumed efficiency, we can calculate the unknown thrust T from equatoin (3) to be
We can check our assumption for ,
using equation (5) or the graph. The power loading P/D² of the
propeller is 1500W/(0.25m)² = 24000 W/m², for which a
maximum efficiency of approximately 97% can be expected at v = 70 m/s
(read from the graph). Thus the assumption of 80% efficiency is not
quite correct and to exploit the momentum theory further, we have to use the
"correct" value. An ideal propeller (without friction and rotational
losses), would deliver a thrust of 20.6 N. The additional velocity can
be calculated by solving equation (4) for ,
which yields a value of = 4.3 m/s,
which is fairly high. For a real world propeller, we can expect to achieve about
80% of the ideal efficiency, resulting in about 78% for this
example.
Performing the same calculation for a lower velocity of 108 km/h
results in T = 40 N, and
= 11.61 m/s. Here we find the optimum efficiency to be
approximately 78%, which leads us to a realistic efficiency of maybe 62%,
which results in a thrust of 31 N.
For a typical, fixed pitch propeller, the largest induced velocity
occurs under static conditions, where the efficiency is small. It decreases with
increasing flight speed, until it reaches zero: no thrust is generated. When the
flight speed is increased even more (e.g. by diving), the propeller acts like a
windmill: it tries to turn the engine, which might be fatal for the engine.
Using
the quite simple momentum theory, we can already deduct important
information about the performance of propellers. We can study the influence of
the propeller diameter on efficiency as well as how it depends on flight speed
or the density of the air (corresponding to a certain altitude). We learn, that
an efficient propeller should have a small power loading per disk area, i.e. a
large diameter is required.
The momentum theory does neither take the planform of the blade into account nor the characteristics of the airfoil sections. For the design or the analysis of a propeller more sophisticated models are necessary, but the momentum theory always gives a good estimate for the maximum efficiency which we can expect.
It is possible to extend the momentum theory to include rotational losses, which results in an additional efficiency loss of 2 to 5 percent for typical propellers. These losses depend on the velocity of rotation and favor low torque, high rpm conditions.
Last update of this page: Septwember 29th 1997
Where do you want to go now?
Propulsion by Propellers 
Design a Prop 
Optimum Propellers
Equivalent Multiblade Propellers
This page has been updated on November, 6th, 1996.
Last modification of this page: 21.05.18
[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.
Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.
It might take some time until you receive an answer
and in some cases you may even receive no answer at all. I apologize for this, but
my spare time is limited. If you have not lost patience, you might want to send
me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose.
Any statements may be incorrect and unsuitable for practical usage. I cannot take
any responsibility for actions you perform based on data, assumptions, calculations
etc. taken from this web page.
© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this
document for a publication, you have to cite the source. A publication of a recompilation
of the given material is not allowed, if the resulting product is sold for more
than the production costs.
This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.
This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.