This document is a transcript of a presentation, given at the «International Nurflügelmeeting des MFC Osnabrück» in May 1993. It was presented to a very mixed audience of modellers and is limited to the basic effects, and not a complete scientific treatment of the topic.

Prologue The Object of Interest Too much Stress?
Bumpy Roads Induced Drag And the Big Guys? Epilogue

Prologue

Most modern high performance flying wing aircraft with nearly elliptical lift distributions have vertical wing tip extensions, called winglets. Flying wings which use the bell shaped Horten lift distribution usually have no need for vertical fins.
Winglets are also used on some conventional aircraft, as they can reduce the induced drag similar to an extension of the wing span. Compared with the span extension, winglets usually produce lower additional bending moments in the wing spar, which makes them useful for retrofitting existing wings without increasing the mass of the basic wing.

In 1992, the DLR Sailplane Symposium at Stuttgart saw a presentation from Mr. Waibel of the well known Schleicher sailplane factory. He presented interesting results from simple experiments, using a Volkswagen Golf (aka Rabbit), equipped with a winglet. This paper shows the results of numerical studies which were conducted to apply his findings to the winglets of tailless models. It is not the aim of this paper to seek information about the optimum winglet shape and its effect on induced drag, but to understand what happens in the region where the winglet joins the wing and why the reduction in induced drag can be spoiled by additional friction drag in this region. Thus we will concentrate on the boundary layer effects.

The cover page of the 1992 «Competitors Achmer News» I found a detailed technical drawing of three tailless planes with winglets (it could also have been an explosion-sketch, as we call it in Germany, of the prototype flying wing «Delaminator») as shown in the title graphics above. The three tailless planes show interesting corners between the wing and the winglets, even an asymmetric layout, which might be optimized for left turns on the northern hemisphere. This drawing, which was very sketchy due to competition reasons, forced me into a more thorough investigation of this region of flying wing models.

The Object of Interest

For the investigation, a simple flying wing model, equipped with the MH 60 airfoil was defined and a three dimensional panel model of the configuration was created (each airfoil section was represented by 60 chordwise panels, spanwise clustering was used to refine the tip and root regions, resulting in about 600 to 800 panels per half wing, depending on the configuration examined). Only the region close to the wing tip was modified, which resulted in four different configurations:

• a rounded wing tip without winglet,
• a winglet with a large, rounded corner,
• a winglet with a sharp corner, and
• a winglet with a sharp corner, but moved downstream 50% of the tip chord. The maximum thickness of the winglet section is approximately located at the trailing edge of the wing tip.

All winglets had the same airfoil as the wing. The following images show the tip region of these four configurations.

Too much Stress?

The boundary layer is very sensitive with respect to the pressure rise, which occurs behind the point of maximum thickness of the airfoil. If the pressure rises too quickly (which corresponds to a steep velocity gradient), the boundary layer will transition early at best or even worse separate from the surface. Flow separation causes large additional drag.

Comparing the flow field around a single airfoil and the airfoil winglet combination, a fundamental difference becomes obvious: whereas the free airfoil feels a pressure rise in one dimension only, an additional spanwise pressure rise is imposed on the flow in the corner between winglet, as depicted below.

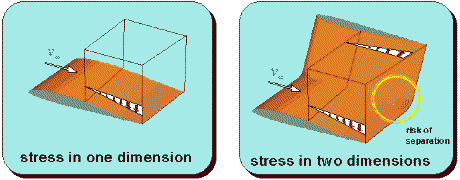
The external flow or pressure field is imposed on the boundary layer flow, which must overcome both pressure rise components in the winglet corner. The result is a high risk of boundary layer separation, if the winglet consists of a simple, bent up wing tip. To remedy this unfortunate situation, the winglet can be attached with an arc segment of large radius, to avoid the rectangular corner. A second way to decouple the pressure rise regions of wing and winglet is to shift the winglet downstream. By doing so, we move the front part of the winglet into the region of the pressure rise of the wing and the winglets pressure rise region is moved behind the wings trailing edge. Thus the winglets region of a favorable pressure gradient (the a region, where the flow accelerates) partially cancels out the wings pressure rise, resulting in a more favorable situation then without the winglet.

The figure below shows the velocity distributions of the wing sections close to the wing tip as well as isobar patterns on the wing itself. The same four configurations are shown.

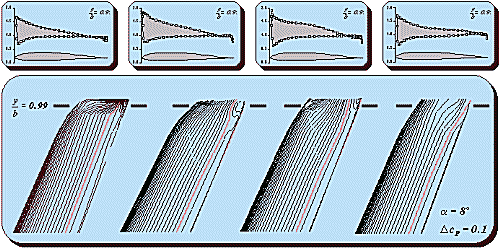
A first impression of the flow field is given by the isobar plots in the lower part of the picture. First it can be seen, that the influence of the wing tip shape is limited to a fairly small region of the wing, maybe 10% of the span. A second observation is the fact, that all winglets hinder the spanwise flow and thus the pressure drop at the wing tip, which is seen in the first configuration, the free wing tip.

The change of the flow pattern close to the tip is also visible in the velocity distributions in a section at 99% of the span, which is shown in an enlarged view below.

Bumpy Roads

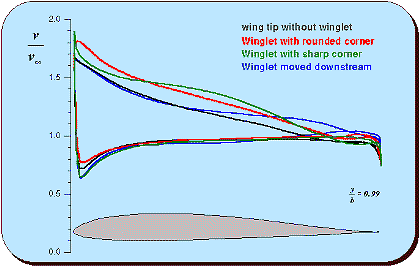
Velocity distributions close to the wingtip of the different configurations.

The graph above shows the local velocity on the surface of the wing, at the 99% span station. The upper set of lines represents the velocity on the upper surface, the curves falling more closely together are for the lower surface, which is of no interest here. Starting with the black line for the wing tip without winglets, we see that all winglet configurations raise the velocity on the upper surface, but at different places.

• The winglet with the smooth, large fairing (red line) shifts the velocity distribution to higher velocities, without a large distortion. Close to the trailing edge, the velocity must reach the value of the lower side, resulting in a steeper gradient there. This configuration is not increasing the stress on the boundary layer very much, but it has a relatively large surface and is more work to build.
• The winglet with the sharp corner (green) shows a quite distorted velocity distribution, with a suction peak close to the leading edge, which can lead to premature transition into turbulent flow. The following region up to 60% of the chord shows a flat pressure gradient, which favors laminar flow, bit it is followed by a steeper velocity drop towards the trailing edge, which increases the risk of flow separation.
• Moving this winglet downstream (blue) shows almost no change in the first 50% of the chord and the velocity distribution up to 80% of the chord is much flatter than the original airfoil. This can lead to a larger area of laminar flow. The pressure rise towards the tailing edge is not much steeper than that of the base airfoil, because the trailing edge velocity is also raised. The result will be similar to the well rounded fairing configuration, probably even better.

Induced Drag

All the investigations above concentrated on the boundary layer and the associated friction drag. Of course the main idea behind winglets on conventional airplanes is to reduce the induced drag, and all the discussion about pressure distributions and boundary layer effects would be incomplete and questionable, if the different configurations would show very different induced drag figures. On the other hand, the main reason for the usage of winglets on tailless airplanes is not the possible reduction of the induced drag, but the search for the most effective arrangement of vertical fins to achieve directional stability - the influence on drag is an additional benefit for tailless planes.

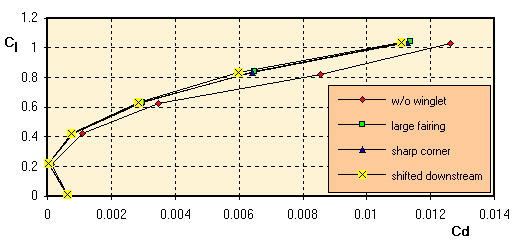
Lift coefficient versus (induced) drag, as calculated by the panel method.

The induced drag polar above shows, that all three winglet configurations show almost identical results in term of induced drag. There seems to be a small advantage for the last configuration, but this is close to the limits of the numerical method. All configurations outperform the free wing tip model - as expected, the drag reduction is getting larger with increasing lift coefficient. The graph does not include the friction drag, which reduces the benefit of the winglets due to the additional surface. Taking friction into account, favors the classical wingtip at low lift coefficients, but the total drag of the winglet configurations will still be lower at higher lift coefficients. For the flying wing, the winglets make a vertical fin obsolete, whose friction drag would have to be added to the drag of the conventional wing tip configuration.

And the Big Guys?

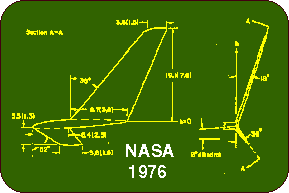
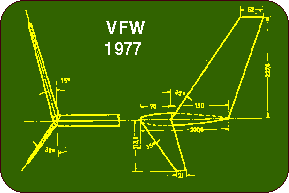
If we look at full scale aircraft with large winglets, we see, that most of them have shifted the winglet downstream, either by reducing the chord length at the root of the winglet (VFW, NASA) or by moving the complete winglet downstream (Voyager). If possible, they add a curved fairing between wing and winglet. The sweep of the NASA and VFW winglets is necessary due to the higher flight Mach numbers, for a model airplane no sweep is needed (only to please your eyes). Also, the dihedral of the winglet is of minor importance as is the small forward winglet-let pointing downward.

Epilogue

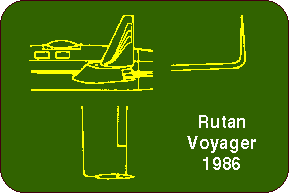
We still have not reached the state of the art with our primitive efforts...

Last modification of this page: 21.05.18

[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.

Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.

It might take some time until you receive an answer and in some cases you may even receive no answer at all. I apologize for this, but my spare time is limited. If you have not lost patience, you might want to send me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose. Any statements may be incorrect and unsuitable for practical usage. I cannot take any responsibility for actions you perform based on data, assumptions, calculations etc. taken from this web page.

© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this document for a publication, you have to cite the source. A publication of a recompilation of the given material is not allowed, if the resulting product is sold for more than the production costs.

This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.

This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.

Impressum       Datenschutz