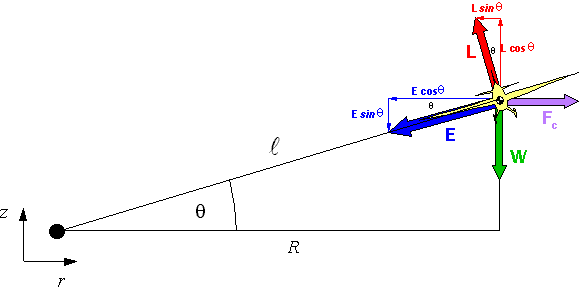
Rear view of a control line model, flying in a banked circle.
Aerodynamics of Control Line Models |
Generally, the flight of a control line model takes place on a hemisphere. The radius of the sphere is given by the length of the control lines. The pilot can control the elevator and thus the height above ground. If a model is flying at a constant altitude, the control lines cut a cone out of space. The inclination of this cone is shown in the figure below as the angle q (greek "theta"). First, we will have a look at the required lift force and the force acting on the control lines.
|
Rear view of a control line model, flying in a banked circle. |
Several forces are acting on the model and all must be in equilibrium. Unknown are the lift force L and the force E acting in the control lines. One thing which is unique to the motion along a circular path is the centripetal force Fc. Note that this force depends on the velocity squared (twice the speed - four times the centrifugal force!). It can be calculated using the following equation:
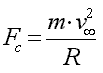 |
where m is the mass of the model and R is the radius of the circle projected into the top view. The figure shows, that two forces counteract the centripetal force Fc: namely the line tension E and the tilted lift force L.
We will now set up the equations for the equilibrium in horizontal direction r:
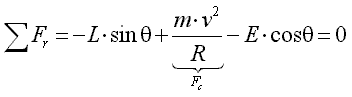 |
and vertical direction z:
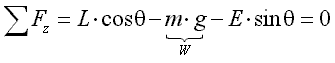 |
We can now solve these two equations for the unknown force E in the control line and the unknown lift force L. The results are fairly simple:
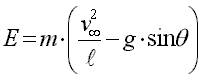 |
and
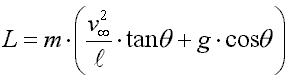 |
for the lift force, which is inclined according to the bank angle.
The expression for the line tension shows, that for a given flight speed, long lines and zero elevation (q =0) produces the largest forces. We also note, that the line force E contains a negative expression depending on the sine of the elevation angle q . For control, one must have tension in the lines. Thus the force E must always be positive, otherwise the model would "drop into the circle". For a given flight speed, the elevation angle q is limited by the formula
|
|
which is interesting as it does not contain the the mass of the model anymore.
| Example: | Given these values speed = 72 [km/h] = 72/3.6 [m/s] = 20 [m/s]; line
length = 15 [m]; gravity acceleration constant = 9.81 [m/s2],
we would try to calculate q < arcsin(2.71).
As the sine of an angle cannot be larger than ±1.0 we cannot find an
angle where the lines would go slack for these parameters. Due to the
selected flight speed and length of the control lines, there will always
be enough line tension, even if we fly an overhead loop. Now we cut the flight speed in half (to 10 m/s) and find q < arcsin(0.679), which has a solution for q = 42.8°. If we would try to fly higher, the lines would go slack and we would lose control. |
If we fly below the horizon (q < 0) the tangent of the angle q in the formula for the lift becomes negative. Thus flying low reduces the required lift. This is because the centrifugal force tries to pull the model back to level flight (q=0). Again, the magnitude of this effect depends on the speed and the length of the control lines. The cosine in the second part of the formula decreases in a symmetrical way about ±q. It tends to reduce the required lift for elevations different from zero, but the first part of the expression usually is bigger than the second one. For typical control line models, the required lift generally increases with positive elevation. The generation of lift also creates induced drag, which is not good if speed is what we desire.
| Symbol | Description | Unit |
|---|---|---|
| E | control line force | N |
| Fc | centripetal force | N |
| L | lift force | N |
| W | weight (mass force) | N |
| r | density of air | kg/m3 |
| q | elevation angle | ° |
| g | gravity constant = 9.81 | m/s2 |
| l | length of control wire | m |
| m | mass of model | kg |
| v | velocity | m/s |
Last modification of this page: 21.05.18
![]()
[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.
Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.
It might take some time until you receive an answer
and in some cases you may even receive no answer at all. I apologize for this, but
my spare time is limited. If you have not lost patience, you might want to send
me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose.
Any statements may be incorrect and unsuitable for practical usage. I cannot take
any responsibility for actions you perform based on data, assumptions, calculations
etc. taken from this web page.
© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this
document for a publication, you have to cite the source. A publication of a recompilation
of the given material is not allowed, if the resulting product is sold for more
than the production costs.
This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.
This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.