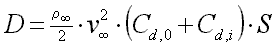 |
Aerodynamics of Control Line Models |
The drag of a control line model is composed of the drag of the model and its control lines. Because of the circular motion and the fact that the the drag force depends on the square of the local velocity the calculation of the power requirements is more complicated than usual.
The drag of the model can be calculated like for any flying aircraft. It is composed of zero lift drag D0 and lift dependent (induced) drag Di. For the drag of the model we obtain the well known formula
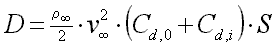 |
The power P required to pull the model through the air at a given flight speed can then be calculated from:
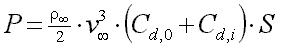 |
Again we need the distribution of the local flow velocity at each radius station as already shown in the notes about flying on a circular path.
|
Top view of a control line model,
flying at velocity |
The local velocity at a radial position r (measured from the center post) is given by
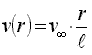 |
|
A segment of a control wire, having
diameter d and length |
If we cut a control wire (having a diameter d) into small segments of length dl we can write for the drag contribution dD of such a piece at a radial station r
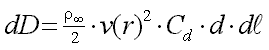 |
To obtain the power consumption we can multiply this expression with v(r):
In general the drag coefficient Cd is a function of the radius because the Reynolds number varies along the radius. If we look at typical values, we see, that this leads to a minor variation of Cd only, so that we can assume Cd=1.15 for all segments along the radius. Also we can safely assume that the wires have a constant diameter d, i.e. they are not tapered.
With these assumptions one can integrate (sum up) the power required by all segments to find the value for the whole wire:
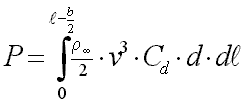 |
The integration along the wire starts at the center post (r=0) and ends at the inboard wing tip (r=l-b/2). The calculation finally yields the following formula for the required power of one control line:
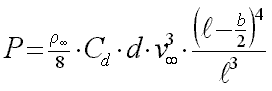 |
The total drag of the control lines can found by integration of dD along the radius and one finally obtains a useful result:
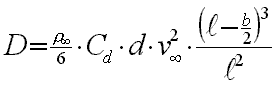 |
It can be shown, that this distributed drag force acts like a single drag force having the same magnitude, attached to a single point at 3/4 of the length of the control wire. This means that 3/4 of the drag force has to be compensated by engine thrust and 1/4 of the drag has to be carried at the center post (i.e. by the pilot).
| Symbol | Description | Unit |
|---|---|---|
| D | drag force | N |
| P | power | W |
| S | wing area | m2 |
| density of air | kg/m3 | |
| b | wing span | m |
| d | diameter of control wire | m |
| l | length of control wire | m |
| v | velocity | m/s |
| Cd,0 | zero lift drag coefficient | - |
| Cd,i | induced drag coefficient | - |
Last modification of this page: 21.05.18
![]()
[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.
Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.
It might take some time until you receive an answer
and in some cases you may even receive no answer at all. I apologize for this, but
my spare time is limited. If you have not lost patience, you might want to send
me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose.
Any statements may be incorrect and unsuitable for practical usage. I cannot take
any responsibility for actions you perform based on data, assumptions, calculations
etc. taken from this web page.
© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this
document for a publication, you have to cite the source. A publication of a recompilation
of the given material is not allowed, if the resulting product is sold for more
than the production costs.
This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.
This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.