Landscape or Portrait ? |
 |
 |
Usually, the size of the vertical tailplane is based on previous experiences and the tailplane volume V. This value is defined as the product of tailplane area times the distance from its aerodynamic center to the center of gravity of the plane. After the area of the vertical tailplane has been defined, it is possible to select different aspect ratios AR for it, making the tail long and flat (low AR) or short and high (large AR).
Similar
to a wing, the drag of the vertical tailplane is composed of friction drag and
induced drag. While the friction drag component is always present, the induced
drag is created only, when the model is in yaw. On the one hand, the low AR
tail has a large chord, which results in large Reynolds numbers and thus low
friction drag coefficients. On the other hand, the vertical tail must develop a
force, whenever the plane is in yaw - this will usually happen during takeoff
and when the plane enters or leaves a turn or has to be controlled in knifes
edge flight. Under these conditions, the low AR tail shows higher
induced drag than the high AR tail. Also, a tail with a high aspect
ratio is more effective, i.e. it creates the required force at a lower yaw
angle.
For a pylon racing model the question is: which aspect ratio is the best, in terms of drag?
The following results are assuming, that the area of the vertical tail is held constant, whereas the aspect ratio is yet unknown. Using the NACA 0006 airfoil, the friction drag has been calculated by Eppler´s integral boundary layer analysis method, with natural transition.
The induced drag coefficient has been approximately calculated by the simple formula
assuming, that the span-efficiency factor k cancels out with the increase of the aspect ratio due to the presence of fuselage and horizontal tail.
Numerical results for a typical F3D model are shown below. When the vertical tail is in a "no yaw" condition, the lowest aspect ratio yields the largest chord and the lowest drag coefficients. But, during the operation of a pylon racing model, small yaw angles, in the order of 0.5 to 1 degrees, will occur frequently. Under these conditions, the increased aspect ratio tails perform better, but it is clearly visible, that it is not necessary to increase the aspect ration to very high values. A good compromise might be an AR of 2 to 3 for the vertical tailplane.
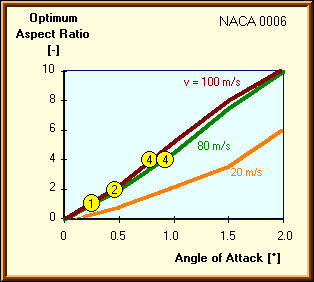 The optimum aspect ratio versus the angle of attack (yaw angle) for two flight speeds. |
 Vertical tails, having the same area, but different aspect ratios. |
It should be noted, that the thin tail planes of pylon racing models operate at supercritical Reynolds numbers, which means, that there is no catastrophic drag increase, when the aspect ratio is increased. The AR = 1 tail sees Reynolds numbers around 1'000'000, whereas for the AR = 4 tail these numbers are more like 500'000. When the flight speed is reduced, say to velocities below 25 m/s, the Reynolds numbers will fall into the critical region. Here, the results may look different, eventually favoring tailplanes of aspect ratios below 2.
Flaps in pylon
racing models ?
Landscape or portrait? How
it all works togetherLast modification of this page: 21.05.18
[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.
Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.
It might take some time until you receive an answer
and in some cases you may even receive no answer at all. I apologize for this, but
my spare time is limited. If you have not lost patience, you might want to send
me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose.
Any statements may be incorrect and unsuitable for practical usage. I cannot take
any responsibility for actions you perform based on data, assumptions, calculations
etc. taken from this web page.
© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this
document for a publication, you have to cite the source. A publication of a recompilation
of the given material is not allowed, if the resulting product is sold for more
than the production costs.
This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.
This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.
