Propulsion by Propellers
Propulsion by PropellersThe thrust of a propeller is not constant for different flight speeds.
Reducing the inflow velocity generally increases the thrust. A reduction of the
aircraft speed down to zero tends to increase the thrust even further, but often
a rapid loss of thrust can be observed in this regime.
That is why the static thrust of a propeller is not such a terribly important
number for a propeller - the picture of a propeller, working under static
conditions can be distorted and blurred.
As long as an aircraft does not move, its propeller operates under static conditions. There is no air moving towards the propeller due to the flight speed, the propeller creates its own inflow instead. A propeller, with its chord and twist distribution designed for the operating point under flight conditions, does not perform very well under static conditions. As opposed to a larger helicopter rotor, the flow around the relatively small propeller is heavily distorted and even may be partially separated. From the momentum theory of propellers we learn, that the efficiency at lower speeds is strongly dependent on the power loading (power per disk area), and this ratio for a propeller is much higher than that for a helicopter rotor. We are able to achieve about 80-90% of the thrust, as predicted by momentum theory for the design point, but we can reach only 50% or less of the predicted ideal thrust under static conditions.
Static thrust depends also on the inflow, influenced by the environment of the propeller (fuselage, crosswind, ground clearance). Measurements of static thrust can be easily done, but the theoretical treatment is very complicated and only possible with a lower degree of confidence than calculations in the vicinity of the design point. Due to local flow separation, the behavior of propellers under static conditions can be very sensitive with respect to blade angle settings and airfoil shape.
To get a picture of the bandwidth of static thrust, several older NACA reports and some publications from model magazines have been examined. The results are combined in the following graph.
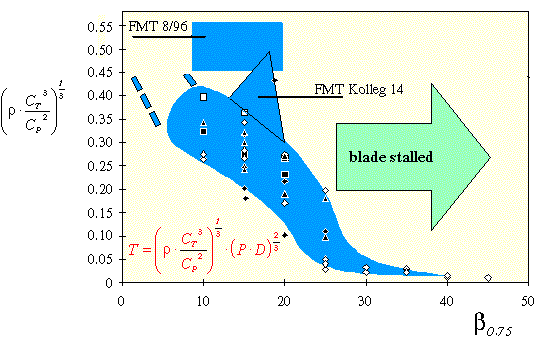
Static thrust parameter (units are [(kg^(1/3)/m] versus blade
angle for different propellers, having 2, 3, 4, 6, and 8 blades. Given power P
and diameter D, an approximation of the thrust T can be calculated. The density
of air has been set to 1.225 kg/m³ (for a description of the coefficients see: aerodynamic
characteristics of propellers).
Of course, the real world static thrust depends on planform and blade angle of the blade and the generic graph gives you a rather wide band of results. One important aspect seems to be the observation of a critical blade angle around 25°. For increased angles, a large part of the blade seems to stall. This effect can be seen on some propellers for high speed model aircraft with large pitch values. After launching the model, it takes some time for the propeller to »catch on«, even when engine and exhaust system are properly tuned. For high static thrust values, a smaller number of blades seems to be better, because (for the same power consumption) they have a wider chord, creating a stronger circulation, being less prone to separation.
As the expression for the propulsive efficiency of a propeller breaks for the static case (the efficiency becomes zero), it makes more sense to use a simple figure of merit like "thrust per input power" if you are interested in static thrust only.
Remark: A hovering helicopter would have a very small blade angle (maybe 5°) resulting in large static thrust values.
| Example: | We have got two different propellers with a blade angle of 10°
and 25° respectively. The first one has a diameter of D = 200 mm,
the size of the second one is D = 300 mm. Which
one would be better suited to build a VTOL aircraft model? How much thrust
can we expect using an .60 engine of 2000 W (assuming a suitable
gearbox)?
From the diagram above we read a static thrust parameter of 0.32 [kg^(1/3)/m], respectively 0.1 [kg^(1/3)/m] around the center of the blue band. To calculate the thrust we have to multiply these values with the power P [W] and the diameter D [m] to the power of 2/3. Performing the calculation for the first propeller (10° blade angle) yields T = 0.32*54.288 [N] and thus a static thrust of 17.4 N, whereas the second, larger propeller delivers 0.1*71.138 = 7.1 N only. Using the same engine in a helicopter with its large rotor of 1 m diameter and low pitch angles, would give us a lifting force of more than 55 N ! This example shows, that the diameter of a propeller is as important for static thrust, as it is under flight conditions. But, for static thrust the blade angle is also very important - probably even more important than for the design point, where a gearbox can match almost any propeller pitch and flight speed quite well. |
Where do you want to go now?
Propulsion by Propellers 
Design a Prop 
Optimum Propellers
Equivalent Multiblade Propellers
Helicopter and VTOL aircraft Statistics
Last modification of this page: 21.05.18
[Back to Home Page] Suggestions? Corrections? Remarks? e-mail: Martin Hepperle.
Due to the increasing amount of SPAM mail, I have to change this e-Mail address regularly. You will always find the latest version in the footer of all my pages.
It might take some time until you receive an answer
and in some cases you may even receive no answer at all. I apologize for this, but
my spare time is limited. If you have not lost patience, you might want to send
me a copy of your e-mail after a month or so.
This is a privately owned, non-profit page of purely educational purpose.
Any statements may be incorrect and unsuitable for practical usage. I cannot take
any responsibility for actions you perform based on data, assumptions, calculations
etc. taken from this web page.
© 1996-2018 Martin Hepperle
You may use the data given in this document for your personal use. If you use this
document for a publication, you have to cite the source. A publication of a recompilation
of the given material is not allowed, if the resulting product is sold for more
than the production costs.
This document may accidentally refer to trade names and trademarks, which are owned by national or international companies, but which are unknown by me. Their rights are fully recognized and these companies are kindly asked to inform me if they do not wish their names to be used at all or to be used in a different way.
This document is part of a frame set and can be found by navigating from the entry point at the Web site http://www.MH-AeroTools.de/.